你知道吗？因为复利效应的存在，福布斯世界富豪排行榜第五名——巴菲特的一生的财富有99%是50岁过后才获得的。
到底复利效应是什么样的一个神奇的东西呢？对于还没见识过复利效应威力的你，我今天立志要将震慑你的三观，拓宽你的财商思维，让你知道赚钱最大的核心理论正是——复利效应！
复利效应小红书
什么是复利效应？
复利效应（Compounding Effect）指的是资产收益率以复利计息时，经过若干期后资产规模（本金+利息的总和）将超过以单利计息时的情况。简而言之，复利就是一直将利息投入在你的资产内持续为你赚取更高的利息，长久下来将可以累积不错的回报。
复利效应不只适用于财富累积的情况上，对于自身的发展与成长同样适用。
复利效应更具体的解释
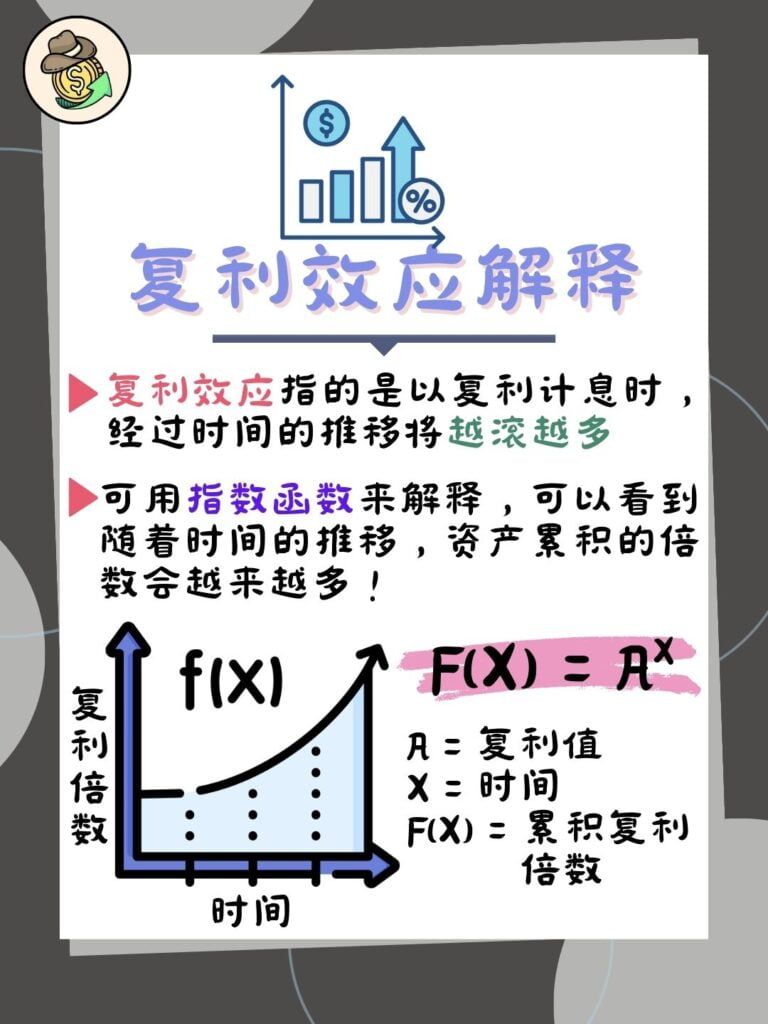
一般上复利成长也会被称为指数型增长（Exponential Growth）。很抱歉得唤起你们对数学的恐惧，我们得跳到高中所学到的指数函数（Exponential Function）来解释这个现象。由于这个高中学到的数学对于财富乃至于你的人生都非常重要，我希望你可以忍着你的睡意学完他！(•́⌄•́๑)૭✧
指数函数
f(x) = ax
上面的 【a = 复利值 】、【x = 时间（年）】、【f(x) = 累积复利倍数】
举个例子，如果小明每年都多存总资产的30%，存了10年；
那么 a = 130%，x = 10，f(x) = 13.79。
这代表10年后小明的资产是现在的13.79倍！
如果现在小明有RM10000，10年后就是RM137900了。图中可以展示小明资产的倍数成长曲线。
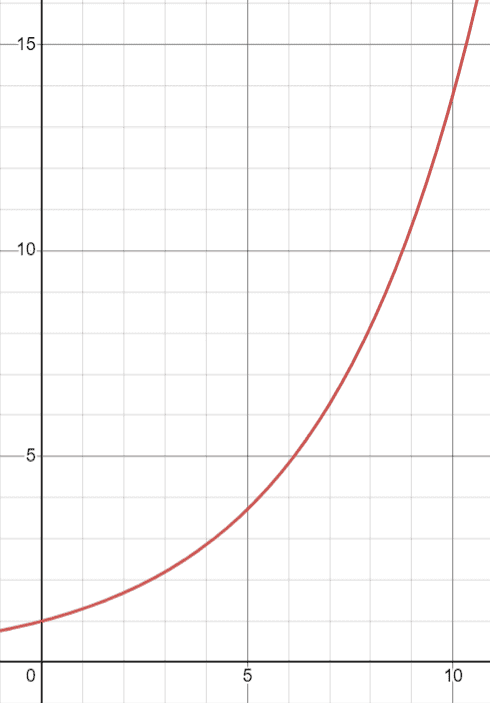
学了上面的指数函数后，聪明的你应该发现了在早期的时候，成长幅度会比较慢，但后期就好像突然爆发一样疯狂地往上涨吧！
没错，这正是”长期主义“的核心观念，只要重复坚持让你的资产利滚利，你的资产会以非常夸张的速度增长！
投资界里复利效应最强大的公式
看得出来巴菲特应该是在这个世界上最爱复利效应的头号粉丝了吧！
他在里面暗喻了2种物品，即湿雪及长坡。
湿雪指的是一个优质的公司，其中获利能力优异最为重要；长坡指的是未来有成长前景的公司。
在我的观点，这段句子还少了两个重要的元素，那就是早期需要一直填雪及时间。
填雪指的是那个雪要达到足够的重量才可以滚得更快，意思是如果早期的资本量不够大，那么再怎么优异的公司为你赚取的报酬都不能覆盖掉你的成本，因此你需要学着存钱让自己的资本大到足够赚取很高的回报才有意义。
巴菲特的黄金搭档——查理 · 芒格，给了一个比较具体的数字，那是$100,000。在他认为，$100,000是最难达到的数字，而后的金额都会比较容易达成的，因为你的$100,000投资后都会比较容易赚比较高的回报金额，甚至会超过你的每年会存的钱，所以基本上过后你都不必再存钱进去了。因此不管怎么样，尽量存到$100,000对于芒格乃至于我们大家都可以是一个重要的里程碑！
时间则比较直观。如果你认为你投资的资产因为市场传出不好的消息，要下跌而及早卖出。但是回过头来发现它反而涨了20%，你就错过了一大波的涨幅了。因此如果你相信这一家公司是好公司，那你一定要坚定地持有让它用时间来滚雪球。
这里提供一些巴菲特认为资产应该卖出的条件：
- 当初你买那家公司的理由已经消失了，例如：买A公司因为它有研发氢能源汽车，认为这是未来的趋势，但是突然管理层告诉股东们他们因为这个项目太烧钱了而砍掉了这个项目。由于不在研发氢能源汽车了，所以你应该把它卖掉。
- 有更好更高回报的投资标的。
- 你的股票价值已经被大幅高估了。
复利效应是把双刃剑？！
复利效应在好的方面真的可以变得很好，但同时在坏的方面也可以变得更坏！
拿一个经典的例子说明：
这个数字的出现正是由下面的公式推导而出的：
1.01^365 = 37.78
0.99^365 = 0.03
先说好，这其实算是一个毒鸡汤啦，因为没有任何一个人可以每天都持续成长1%，也没有一个人每天都会退步1%的。因此不必要将这个名句当成你的人生名言。如果要知道为什么我会这么说可以点击下面的按钮阅读。
但是上述名言也不无道理，如果你真的一直不改掉你的坏习惯，例如抽烟。每天最少一根真的会破坏你的健康不少，甚至最后可能患上肺癌然后需要非常大量的金钱就医，得不偿失。
这里的小结是即便你要放松，你可以选择偶尔地放肆，但一定不要每天都做不然人财两空的窘境也不是不会发生的！
复利效应在财务上的双刃剑
最典型的例子莫过于负债的复利效应。
今天如果你用信用卡，借贷利率是18%，你只需要4年的时间就会将你的债务翻倍了！
所以借贷是一个需要仔细三思的事情，如果借贷的成本超过了你将来可以获得的收益（投资获利或满足感都可），宁可不要借！
如果不幸借了而且债务也越滚越大，可以点击下面的按钮参考如何处理你的负债。
72法则
72是金融学上一个非常神奇的数字。它可以让你计算出如果你的回报率每年都一样，多少年可以让资产翻倍。
时长 ≈ 72 ÷ 年化报酬
举个例子，如果你的资产的年化报酬率是1%，那么你需要：72 ÷ 1 = 72年才可以达到；如果是8%，那么你仅需要：72 ÷ 8 = 9年就可以翻倍。
证明的方法其实并不难，只需要用：（1+年化报酬）^时长 ≈ 2 就可以了。
用回上述例子，1% ：1.01^72 = 2.05 ；8% ： 1.08^9 = 2.00。
因此我们可以大概推断出每个年化报酬率多久可以达到资产翻倍。
| 平均年化报酬率（%） | 翻倍时长（年） |
|---|---|
| 1 | 72 |
| 2 | 36 |
| 3 | 24 |
| 4 | 18 |
| 5 | 15* |
| 6 | 12 |
| 7 | 11* |
| 8 | 9 |
| 9 | 8 |
| 10 | 8* |
| 11 | 7* |
| 12 | 6 |
| 13 | 6* |
| 14 | 6* |
| 15 | 5* |
| 16 | 5* |
| 17 | 5* |
| 18 | 4 |
*有小数点的一律进位+1
现实可达预期
在看答案之前，你认为年化的投资报酬率应该是多少才算合理呢？
一般上来说，一个普通人的年化投资回报率可以达到6% ~ 8%的回报率已经是不错了，如果可以达到8% ~ 10%的已经算是普通人里的高手了。有的人甚至可以达到每年的报酬率超过10%，这需要承担非常大的风险，但是可以达到怎么高的回报率凡人比较难达成。
做个小结，一般上我们普通人都会将8%设定为目标，当然如果真的有能力的也可以试试把目标区间往上移啦！
了解了合理的年化报酬率的目标后，以下介绍一个超好用的免费资产组合模拟回报的网站，点击下面的按钮可以进去看看。
因为这个回测的时间足够久（最少有超过10年的回测），这个可以让你们较准确地知道如果你投资在什么商品应该预期的回报是多少。（如果不是很清楚里面地资产有什么可以点击下面的按钮复习！）
此外，你也可以看到不同的时期你的资产的涨跌幅，让你可以知道自己到底能不能承受下跌，更重要的是一个正回报的回测可以让你更加坚定地持有你的资产，从而真正地实现”滚雪球“的效益。
那我们废话不多说，直接进入教学吧！（专注在新手应该注意什么而已，其他的需要了解更多的金融知识后才会比较了解）。
基本功能介绍
例子（一）
第三页里的通胀调整后的数字可以看得出非常惊人的下滑，如果不清楚通胀是什么的可以点击下面的按钮了解了解~
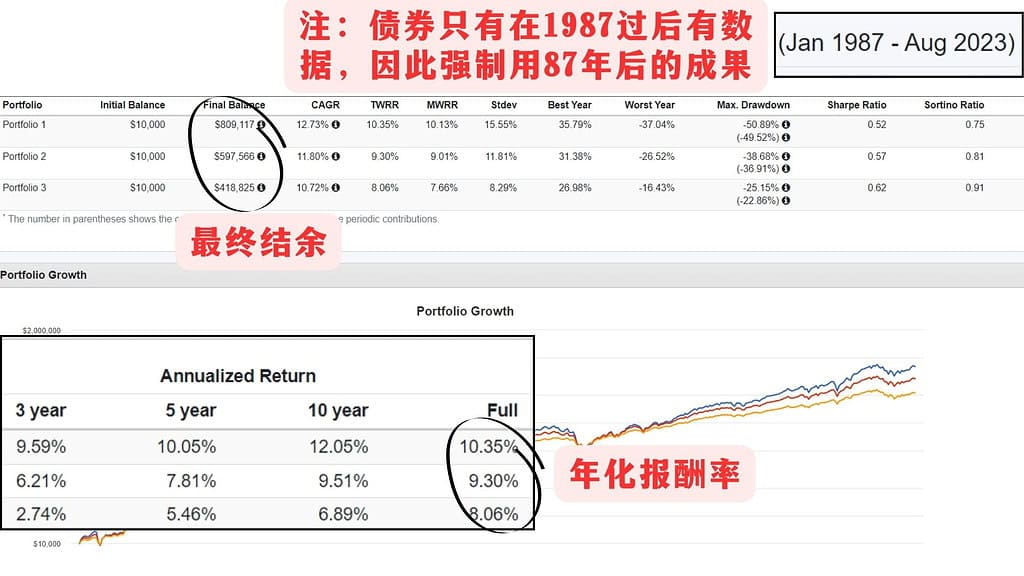
例子（二）
从例子（二）里可以看出，CAGR的数字和年化报酬率不一样，这是因为如果有现金流的改变（流入/流出），TWRR的计算年化报酬率的方法更为准确，如果有兴趣学TWRR和MWRR之间的区别的可以点击下面的按钮学习。
此外，经过时间的推移，即便年化收益率只差1%，累积下来会是非常巨大的差别的，因此这就是为什么巴菲特说要找“湿雪”的原因。有谁能想到，在例子（二）里你总共投进$46000（初始的$10000+36年的$1000）而已，经过时间的复利居然滚出了$800000？！（如果计算通胀后依然还有$300000的购买力）
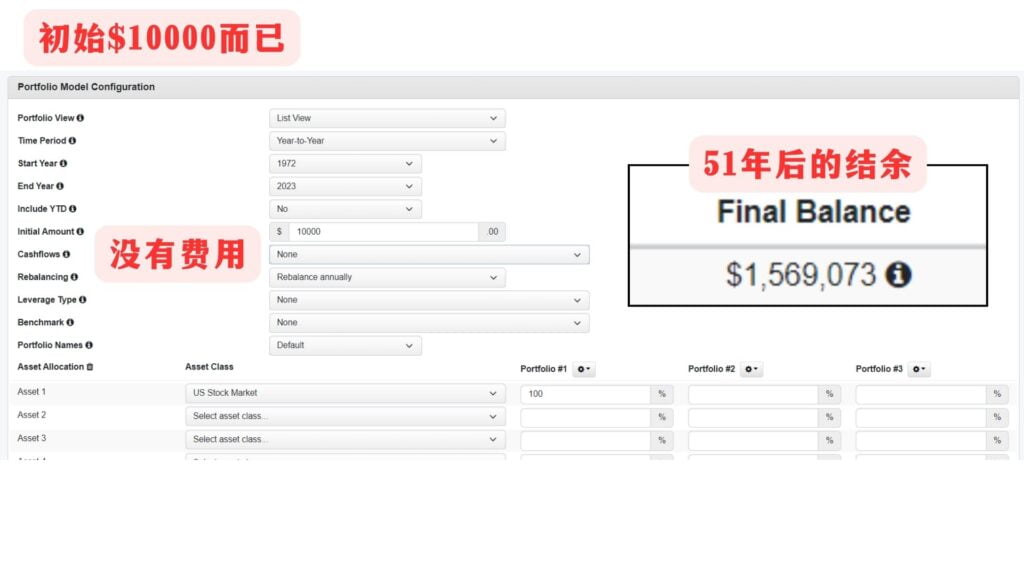
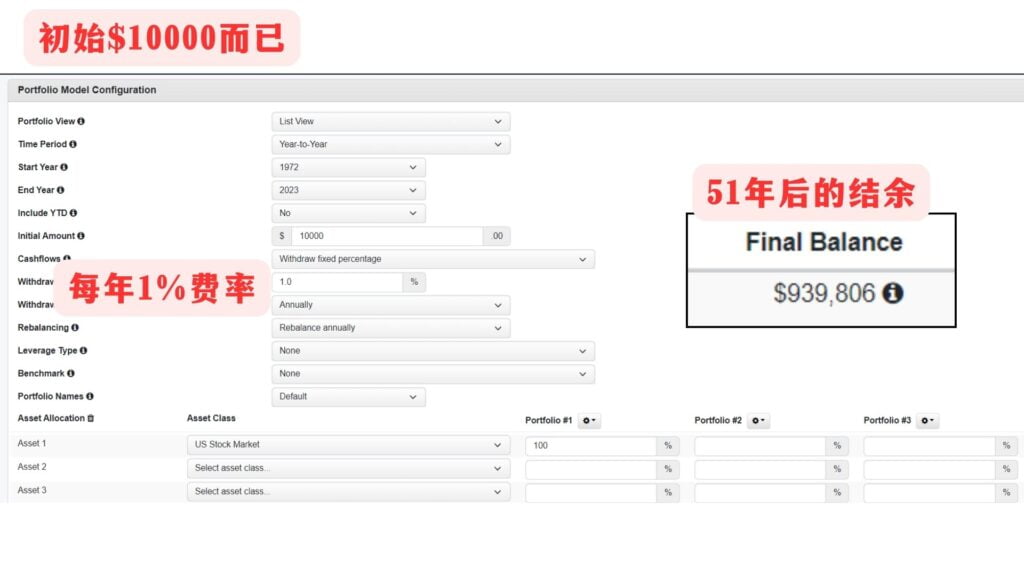
例子（三）
例子（三）探讨的是1%的费用率差别到底有多大。
图一可以看到的是$10000经过51年的复利有了$1569073的结余资产，而图二剩下$939806，中间居然蒸发了$629267！
因此，真的不可以小看1%的差别，时间一长你损失了多少不敢设想。
小结
如果有人问说最好的时间投资是什么时候？我会回答：“第一，是10年前；第二，是现在”。即便你可能现在40~50岁了，现在开始总比没有开始来的好，更何况你还有非常多的时间可以进行复利呢！
相信学完今天关于“复利效应”后应该是拥有了对于复利强大的威力有一些头绪了吧~
只要有足够长的时间让它去利滚利，那么往后得到的收益真的会非常夸张的！
但是切记，一定不要贪，网上拥有许多的“快速致富”的骗局，往往有人因为经不住推销员的甜言蜜语就不幸沦为了韭菜，让自己存下的血汗钱付诸流水。一定要学会自己判断真伪，锻炼自己的独立思考能力以防自己受骗。
以上便是这篇文章的所有内容啦~ 希望你看完了这篇内容有所收获，知道达到财务自由的关键钥匙——复利效应，你对于你未来的人生更有憧憬和掌握权哦！如果这篇对你有所帮助，请帮我分享出去让更多人知道这个宝贵的知识啦！
免责声明：此文章內容仅为教学、分享及参考的用途，而非专业的投资建议。